In part 2 of this 4 part blog series I will walk you through the evolution of ideas that led to our final equitable sales territory algorithm. Then, I will explain how we prepared the data to execute this algorithm.
Before touching Alteryx, we deconstructed the task we needed to undertake. Ultimately, we needed to strike a balance between 2 things:
- To split the UK up into 9 groups of equal sum turnover (one for each salesperson).
- To construct practical sales territories that our 9 salespeople could cover
Both of these tasks can be done relatively easily in isolation in Alteryx, but how do you execute both simultaneously?
This solution is not straightforward, and ultimately some equity in sales opportunity may need to be sacrificed to construct territories that are practical for the salesforce.
The most granular geographical units we were dealing with were postal districts, of which there are roughly 2600 in the UK. We needed to find a way to aggregate these together or divide them up somehow in a systematic way that balances the 2 aforementioned conditions.
Tile tool?
Initially, we experimented with the Tile tool, to see if this could group postal districts into clusters of equal value. The Tile tool works by grouping data into sets (tiles) based on a selected variable, with the option to divide sets so they have an ‘Equal Sum’ of the chosen variable (in this case turnover).
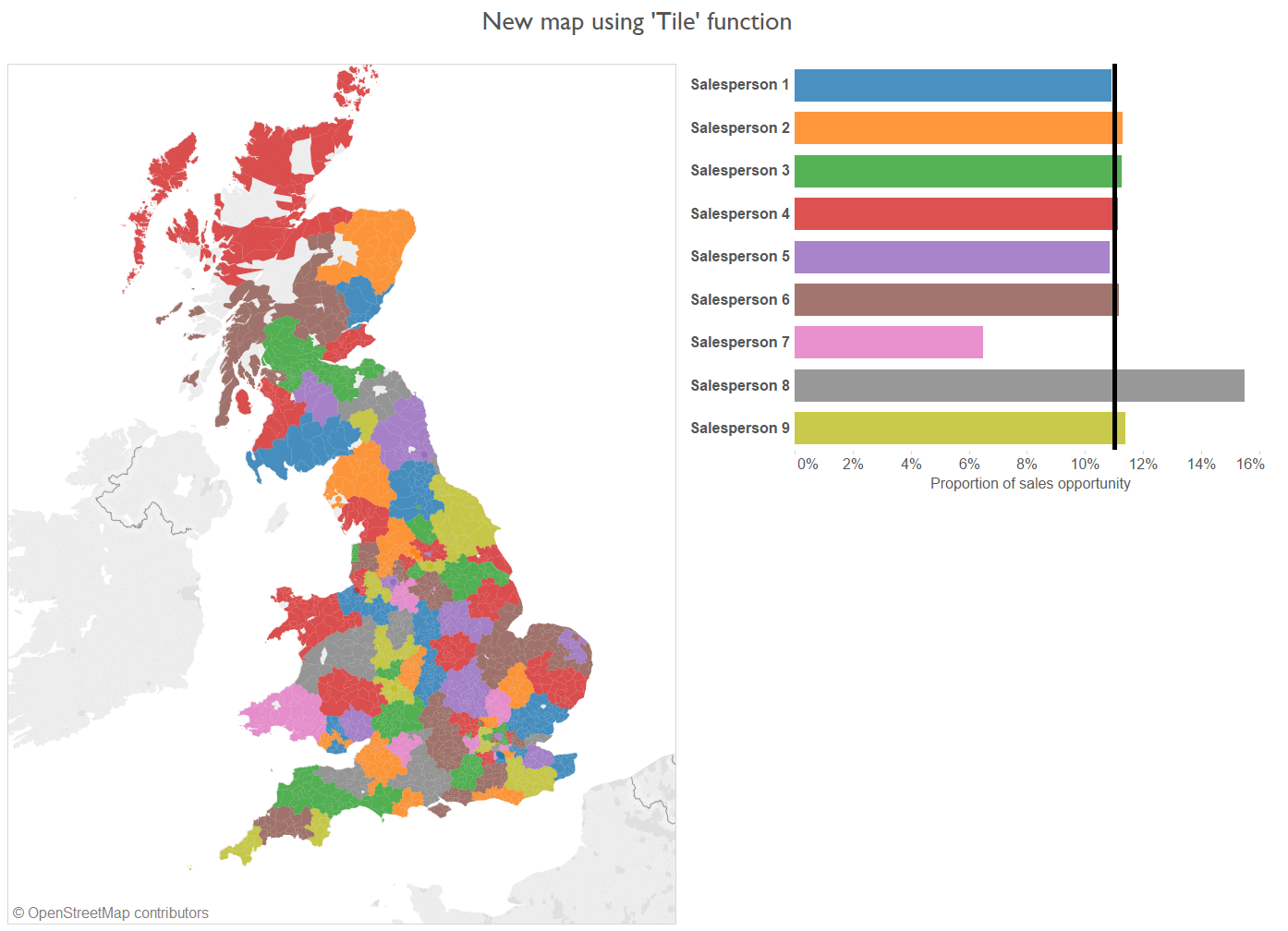
Re-drawing sales territories based on the Tile tool results in greater equity in sales opportunity – as illustrated by the bar chart to the right – but also high interspersion of territories.
This technique more or less satisfied this first condition, but provided no means to instruct Alteryx to cluster districts contiguously in order for salespeople to be dealt practical territories. Instead, territories were haphazardly dispersed across the country, creating a clown vomit effect.
Tile tool – with geographic sorting?
The Tile tool provides the option to sort the data by a second variable before it is allocated a tile. Experimenting with sorting by a concatenation of ‘Salesperson_name+latitude+longitude’ returned the following output:
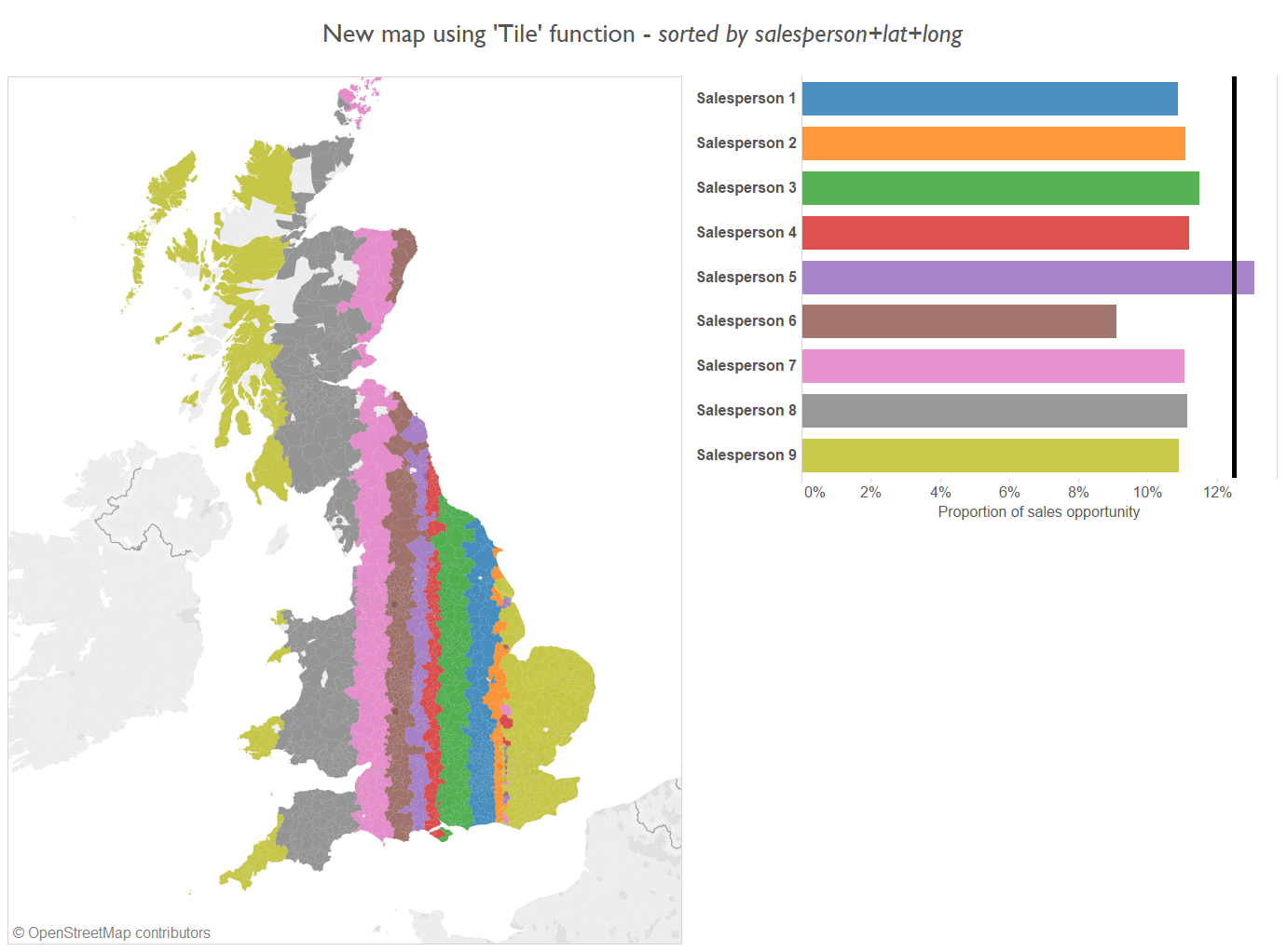
Equitable, and geographically aggregated, but highly unpractical.
Back to the drawing board.
For practicality we need to limit the distance our salespeople have to travel. An ideal scenario would be for each person to be allocated a roughly circular blob of equal sales opportunity. Therefore, it looks like we need to find a way to construct territories in a more radial pattern around a fixed central point for each salesperson.
One to achieve this would be to identify the centroid of each salespersons existing range. This centroid will in turn act as a seed (or anchor) for which the territories will grow around, by attaching adjacent postal districts.
This process of ‘geo-aggregation’ can be done in an equitable manner by taking the person with the lowest sales opportunity (i.e. lowest turnover of all prospective customers in the postal district at their centroid), and assigning them the next closest district to their centroid.
The salesperson with the worst deal, now gets access to all the businesses within this new district.
Then, following this adjustment, we can re-calculate which person has the lowest sales opportunity and repeat the process. In this way, we are continually expanding territories in a way that is equitable, by repeatedly assigning an additional postal district to the guy with the current worst deal.
This sort of repetitive functionality can be automated in Alteryx using an iterative macro, which will be covered in the next blog post.
In this remainder of this blog post, I will talk you through the process to prepare your data for the iterative macro.
Preparation of data for the ‘Geo-aggregation’ iterative macro.
Here, we need to prepare 2 data tables, which will become the inputs of our iterative macro.
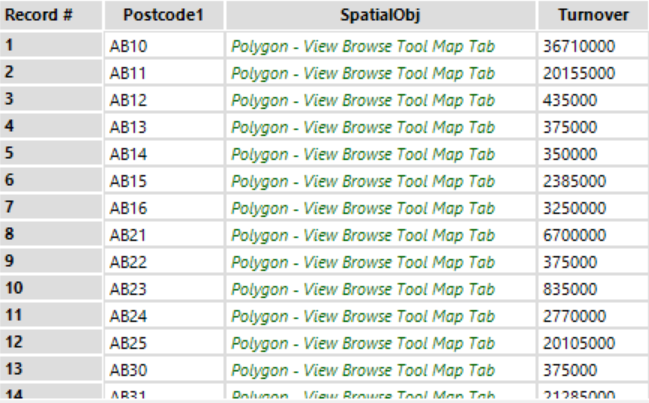
1. The list of ~2600 postal districts, their associated polygon shapefiles, and sum turnover of prospective customers within them. The macro will dip into this list to repeatedly find the district nearest to the salesperson with the lowest sum turnover.
2. The list of salespeople, their home postal district, associated centroids (spatial points), and sum turnover within their home postal districts. This will be used to inform the macro which salesperson should be assigned an additional postal district next.
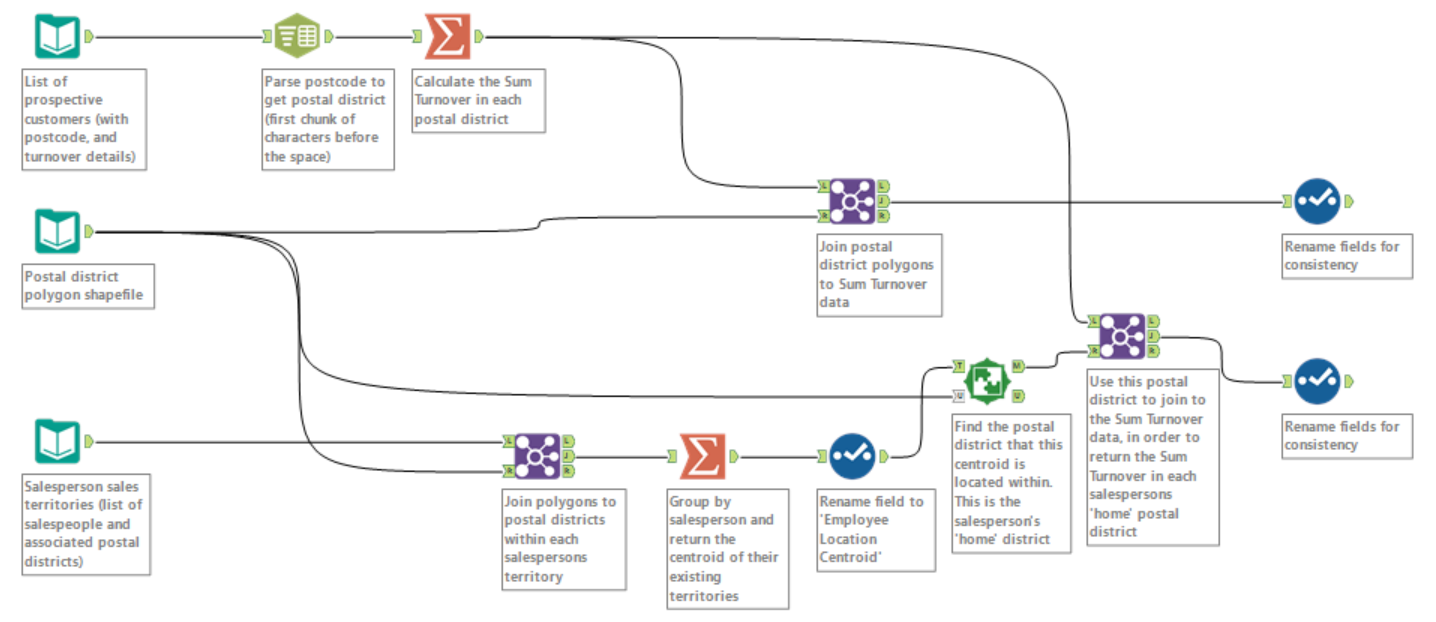
The top part of this workflow takes the list of prospective companies, chops off the second part of their postcodes – which have a format of xxx(x) xxx – to return the postal district, and then sums the turnover of prospective customers within each postal district.
The output is the following table, which will become the first input into our iterative macro.
The bottom part of the workflow takes the existing sales territories, finds the district at the centre of each territory, and adjoins the sum turnover of prospective customers within this ‘home’ district.
The following results table will become the second input into the iterative macro.
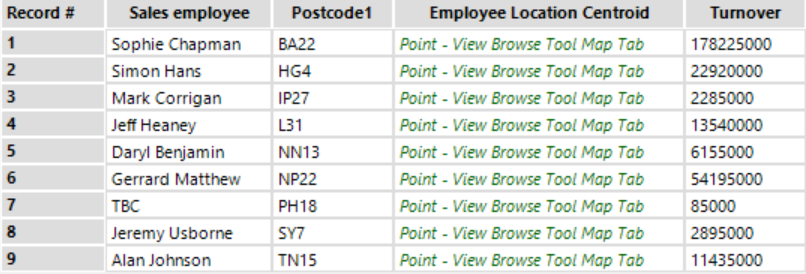
Now the data is all prepped to be fed into the iterative macro.
In the next blog post, we’ll explain how we set up the iterative macro to perform our ‘geo-aggregation’ algorithm.
