For my second blog post about predictive analytics I going to speak about Sales forecast.
Maybe I am interested to understand what drives Sales in my business. I have many stores running for years and now I would like to make a prediction about 10 new potential stores and then decide which one to open first. I assume in this case that demographics will give us some insights about sales.
So just to make a link with Part 1 of Predictive analysis, in this case there is a target variable (dependent or explained field) and some predictors (independent or explanatory fields).
In order to do this we test 3 different statistical models and find which is the best in predicting Sales. Then we will use that model to forecast sales for our 10 new potential locations.
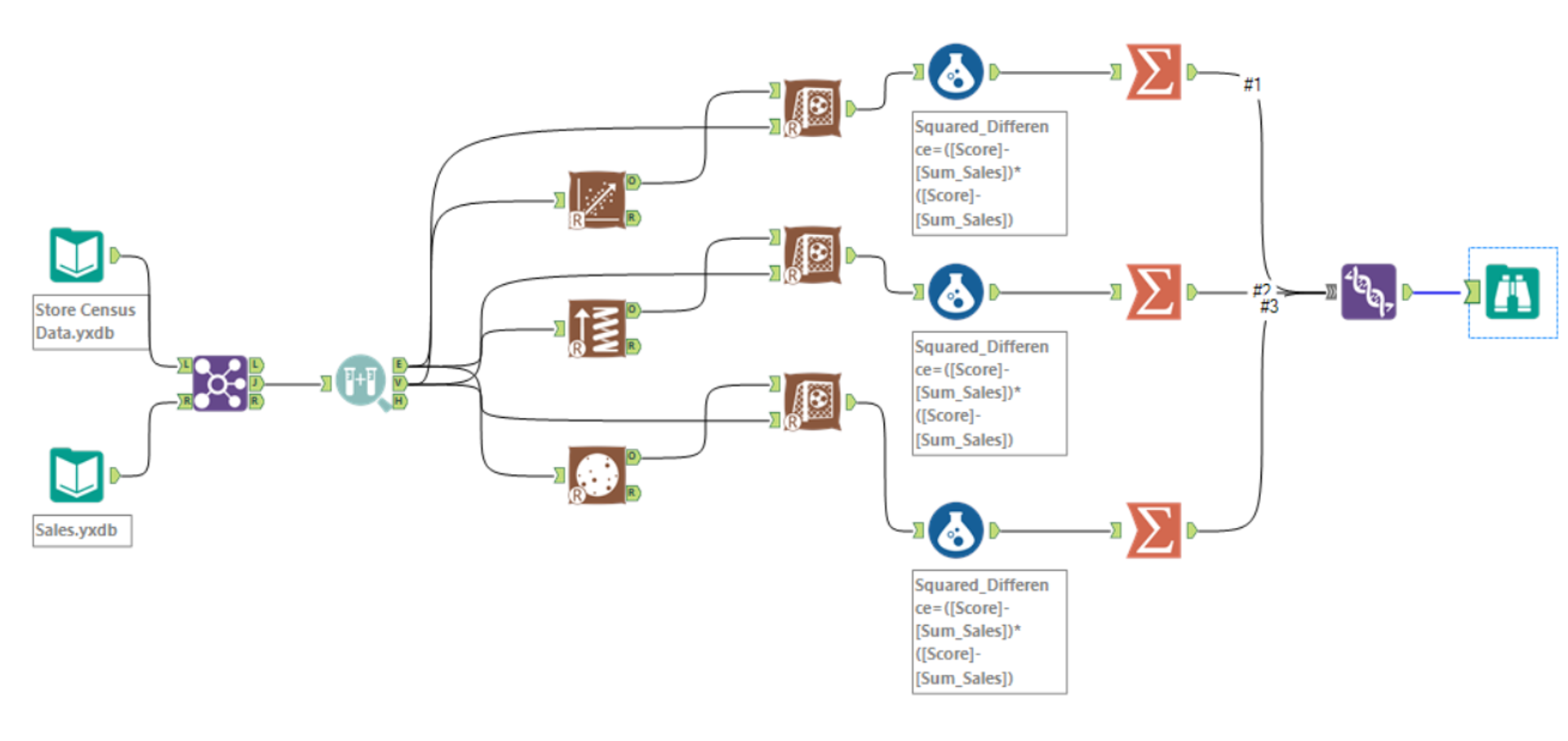
First I need two datasets: Store Census Data (for Demographics) and Sales (for Sales). I join them together.
Sales is quantitative, all our predictor fields are quantitative too so we will identify drivers by regression type models (linear regression, Boosted model, Spline model).
A really important thing to remember when you use regression type models is to create Samples in order to train your predictive models on a subset of data (Estimation sample) and validating the models on another subset (Validation sample). Anything not categorized in these two gets to the Holdout sample. You have to set the estimation sample percent (if you use the boosted model this has to be at least 80% of the records) and the validation sample percent.
Now we run three different models:
- Linear Regression tool
- Boosted model
- Spline model
Here remember to select the target variable and the predictor variables.
Now use the Score Tool to add the score of each model to the DataStream.
Now we have the actual Sales by Store (original data) and the predicted Sales by Store (from 3 models). To test the goodness of our prediction we use a formula Tool and we calculate the difference between predicted and actual sales. More precisely we want the squared difference of:
([Score]-[Sum_Sales])*([Score]-[Sum_Sales])
or
POW(([Score]-[Sum_Sales]), 2) just another way to return x raised to the N power
Why squared?
Predicted value can be either above or below the actual, in total these differences may add up to zero. Basically the square corrects this.
Then you summarize and union them. You choose the model with lowest error (smaller difference).
Now that we know what’s model is best for us (in my case boosted one) you need to put a input data with the potential locations, add a score tool and create an output.
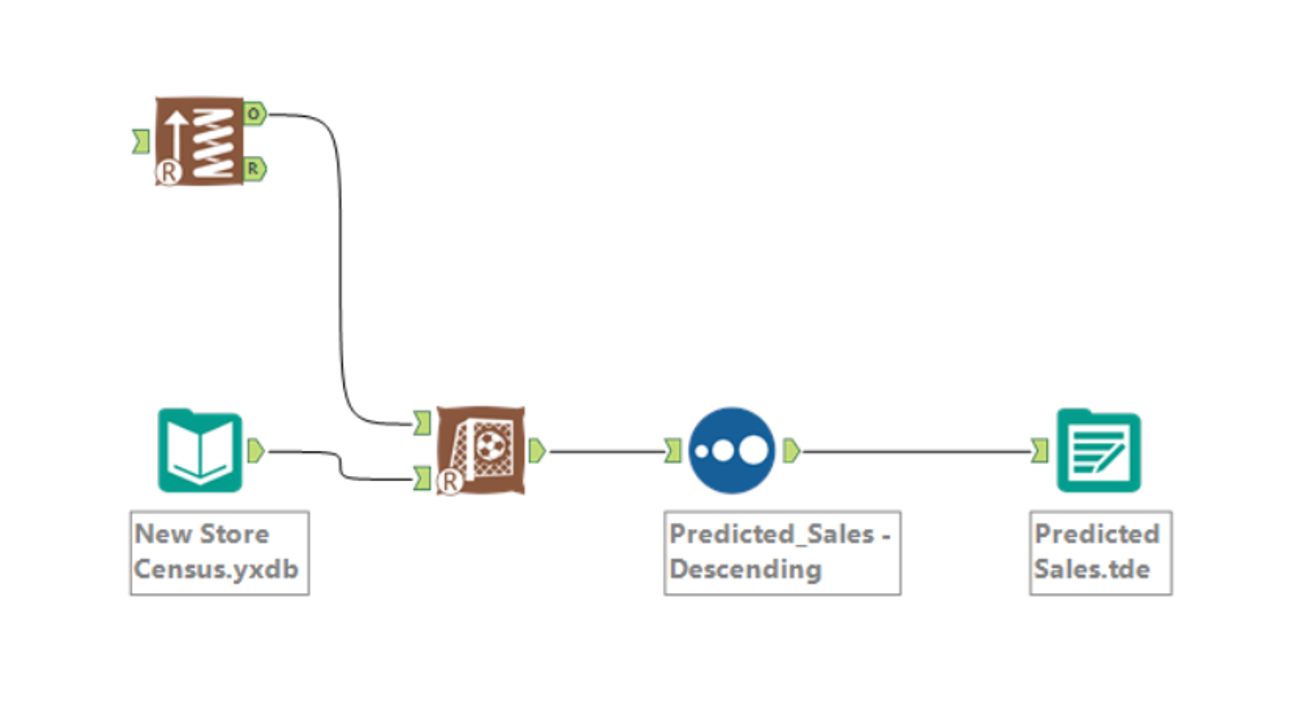
Now tell me which store I should build!
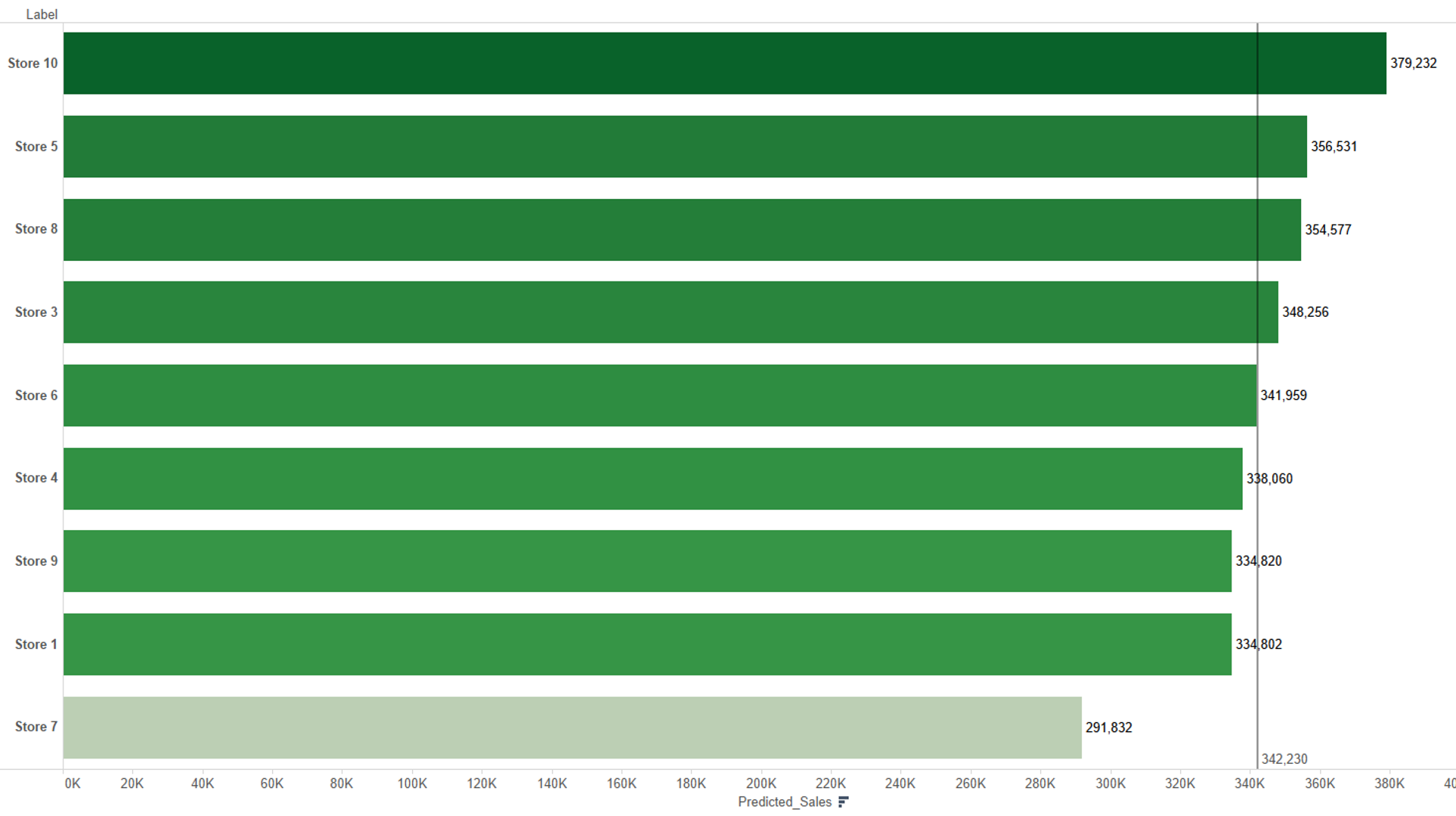
If we open Tableau with the predicted Sales file that we have created in Alteryx, I drag predicted sales in columns and the new stores in rows and if I sort them by descending order I get the view from the highest predicted sales for location to the worst one.
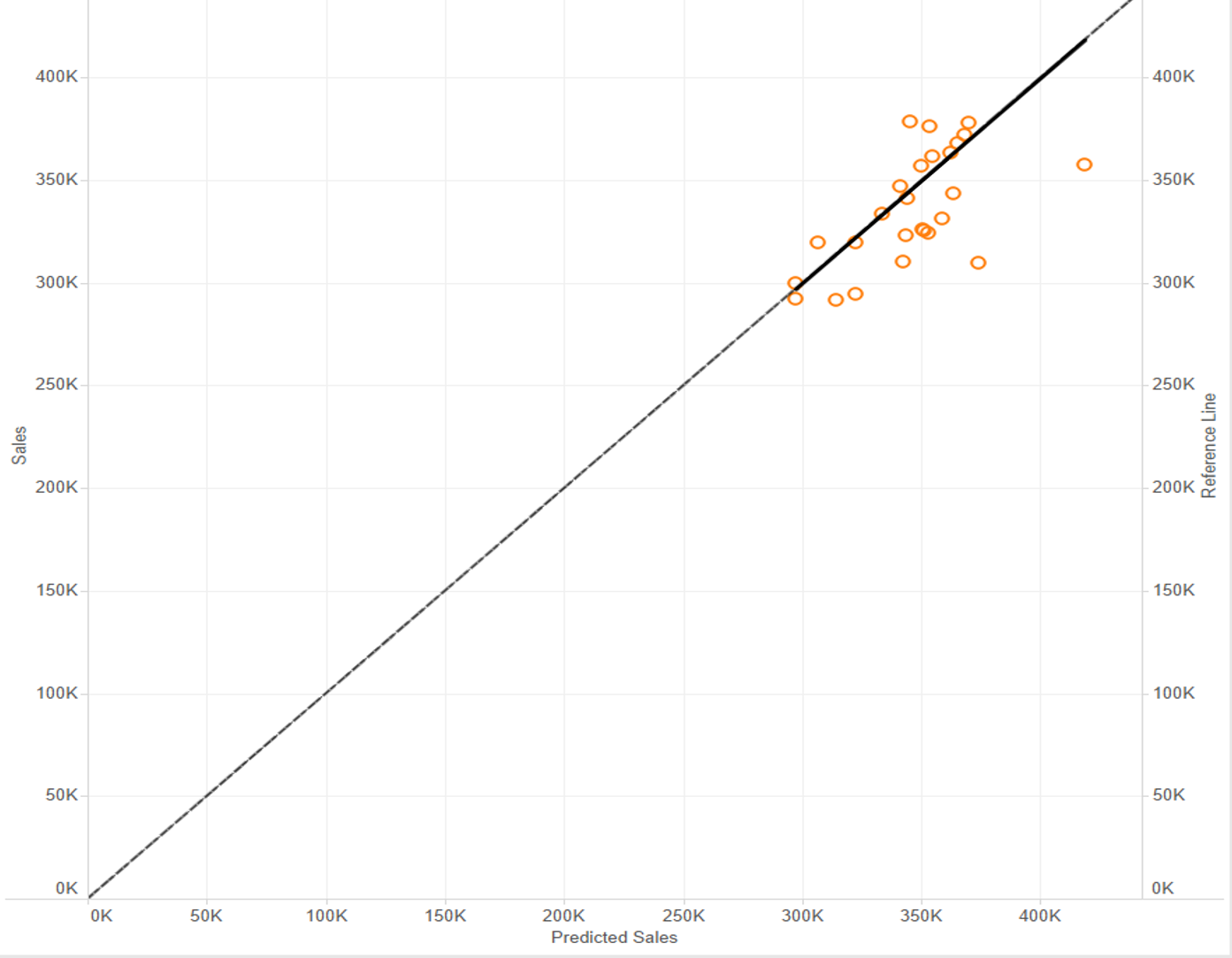
I also can compare the predicted sales against the sales creating an output data tool after the boosted score and open it in Tableau. You make a scatter plot with the two measures, Store ID on level of detail.
Create an artificial 45 degree reference line:
sum(PredictedSales) on columns and sum(Sales) in rows, then create a calculated fields called reference line where you write predicted sales. Then you drag it in rows next to Sales, make a dual axis, synchronize it and change the format of the reference line in a line. Then right click on the line –> trend lines –> show trend lines.
The Stores (circles) scatter about evenly around the reference line meaning that the model is not skewed (not systematically over- or under predicting sales).
You can download the workflow here.
Have fun!
