
Unlike Tableau, Alteryx does not have a function to rank the data by some condition, so we need to create our own function to define the rank. And the tool that we are going to use is Multi-Row Formula tool the Preparation tab (dark blue).

To demonstrate, we shall use the Billboard Top 100 data set from Alteryx weekly challenge #189.
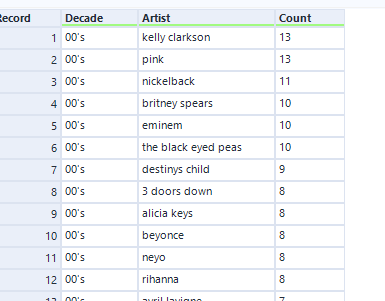
The following is the partial results that we will use to define (various) rank.
The general principle is very straight forward:
1: Sort the (numerical) measure used to rank.
2: Decide type of rank to be used
3: Calculate the rank from 1 (most commonly, ascending) according to 2.
Step 1 can be done easily with a Sort tool, as shown above, ascending by Decade, then descending by Count.
Step 2 has a few more options, they are various methods of handling equal ranked item. For a more detailed comparison, we can have a look at the Wikipedia link below, or we can just use examples to see the differences.

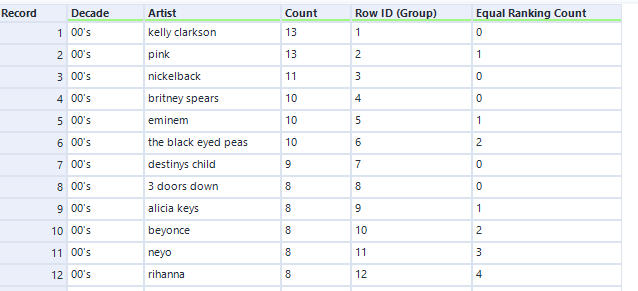
For most of the calculation we need an additional variable to keep track the number of equal ranks. We create use a Multi-row Formula tool to create Row ID to keep track the over position and an Equal Ranking Count for calculation.
Note: Row ID restart count for each group (e.g. group by Decade). If no grouping is needed, then Record ID tool will be suffice.
1. Standard competition ranking
(E.g. 1, 2, 2, 4) In this type of ranking, measures that are equal receive equal ranking, then a gap is left after ranking is applied, but before the normal ranking resume.
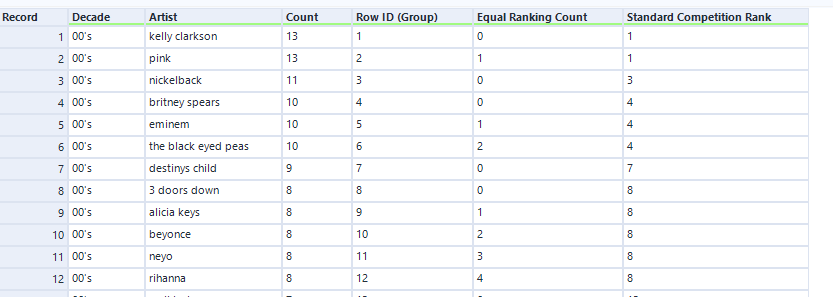
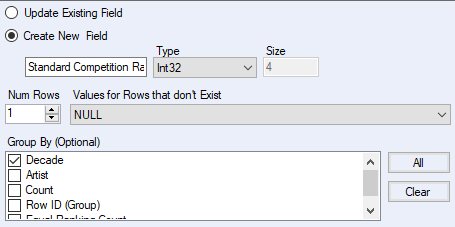
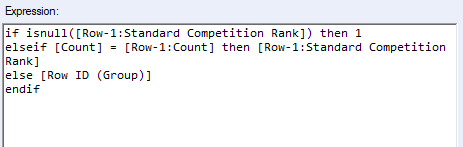
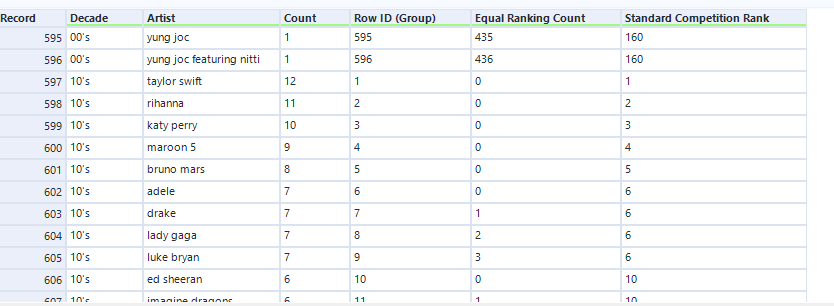
Since we have sorted the data first by Count descending, if previous row is NULL then current row is the top record (i.e. rank one) given our setup for Values for Rows that don't Exist. As we move down the measure variable column, if current row equals to previous row, then they have equal rank, hence we use the previous row rank, else we Row ID which is the position for none repeating rank.
We can also check, the ranking restarts for a new group.
2. Modified competition ranking
(E.g. 1, 3, 3, 4) Similar to previous standard competition ranking, except this time the gap is left before applying the equal ranking.
Note: To be able to do a modified competition rank, we need to know how many rows that have equal ranking, a trick need to be applied with Multi-row Formula, which we shall demonstrate in a separate blog post.
(See Part 2)
3. Dense ranking
(E.g. 1, 2, 2, 3) Similar to standard competition ranking, except this time there is no gap left before or after applying the equal ranking.
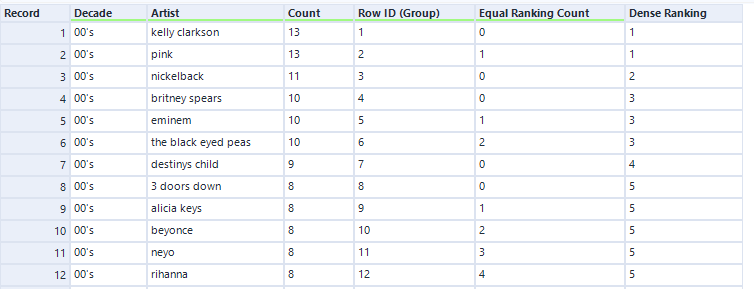
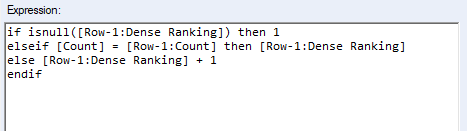
Since we don't need to worry about calculating the gap, we are either copy the previous rank (for equal measure) or +1 to previous rank (for different measure).
4. Ordinal ranking
(E.g. 1, 2, 3, 4) This is basically equal to Row ID. For equal ranking measure, we assign their rank either randomly or by arbitrary but consistent rule, such as alphabetical order.
We can either rename Row ID by a Select tool or create an equal column by using Formula tool.
5. Fractional ranking
(E.g. 1, 2.5, 2.5, 4) Equal measure rows are ranked equally by using averages. The benefit is more in the purpose of statistical analysis, since the sum of rankings are equal to Ordinal ranking (i.e. Row ID), which is not true for other forms of ranking.
Note: Similar to Modified competition ranking, we do need to know how many repeats there are for equal measures, which need to be calculated with a trick, so we shall leave that to a separate blog post.
(See Part 3)
Looking for more guides, tips and tricks in Tableau or Alteryx? Go check out the other blog posts from the Data School.

