
Market Basket Analysis is (an)
Association rule learning that is a rule-based machine leaning method for discovering interesting relations between variables in large databases.
There are three important measures we need to adjust the model, Support, Confidence and Lift.
As much as an additional term defined for this analysis, they are quite easily visualize from Venn diagram. This blog will show the interpretation of them a statistical point view as probability (which they are).
Note: We will not worry about define an association rule here in this post.
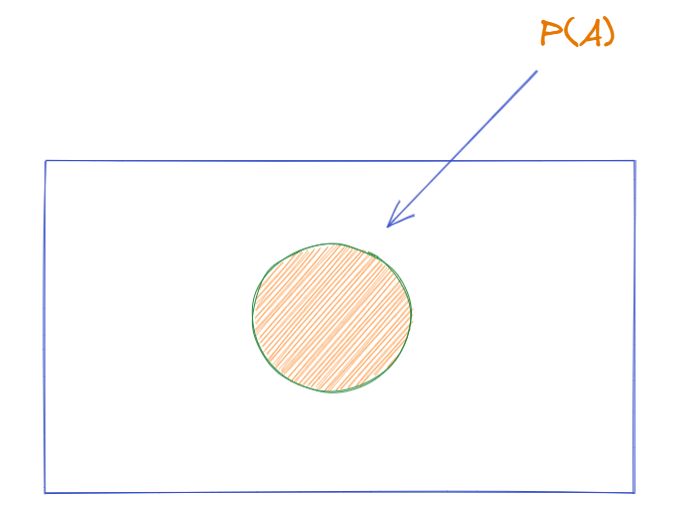
Support:
Within a dataset, i.e. a list of transactions, how many transactions contain item A, so it is just the probability of item A occurring, which we can represent as below. Statistically speaking, it is a frequentist's estimate of the probability.
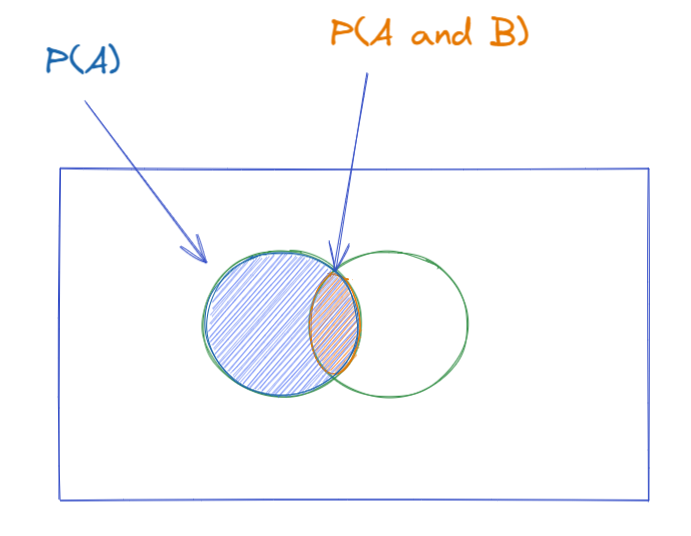
Confidence:
Out of the transactions that contains item A, how many also contains item B. The bigger the overlap, the greater the confidence we have that people who are buying item A also buys item B. Statistically speaking, it is (estimated) conditional probably of item B given item A, i.e. P(B|A).
Lift:
The ratio between Confidence of A and Support B, it is less intuitive with the description, so let's try to visualize it better. First let's see the formula below.
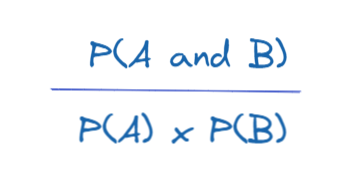
There are two special cases in the above formula.
Independent: If A and B are independent, then P(A and B) = P(A)*P(B)
Mutually exclusive: If A and B are mutually exclusive, then P(A and B) = 0
In the first case, the Lift will be 1, while in the second case, the Lift will be 0, regardless the probability of either A or B happening. Hopefully this makes intuitive sense, if buying item A is independent of buying item B, then know the customer brought item A will offer no support (or confidence) to guess they will also buy item B. If buying the two items are mutually exclusive, then buying item A will immediately indicate the customer will not buy item B.
Note: for the following writings we will assume P(A) = P(B) to simplify the visual.
Case 1:
P(A) overlaps P(B), then the formulas for Lift simplifies as follow
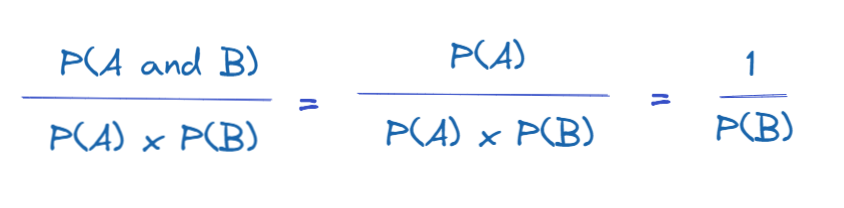
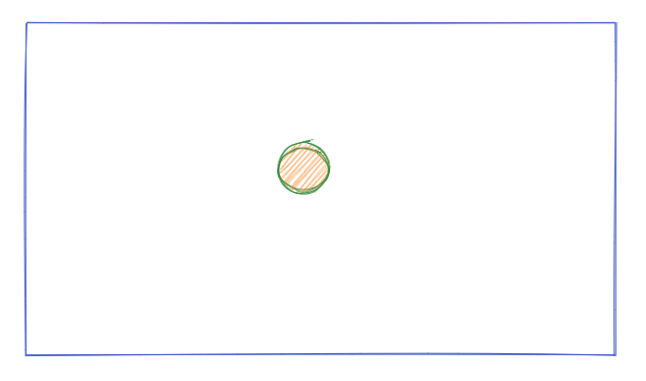
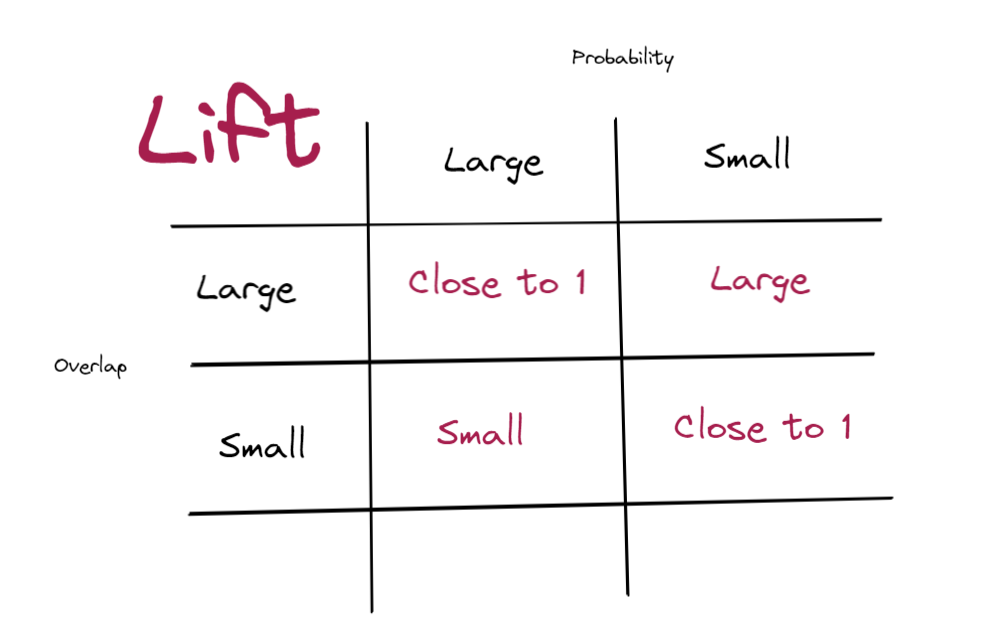
In the case P(B) is large (say 0.9), the Lift is closer to 1 (i.e. 1/0.99 = 1.01). Buying item B is very common (also item A), so even if they do both appear in a single transaction, it is more likely due to commonality rather than association, so the Lift from one to the other is close to no association (independent).

In the case P(B) is small (say 0.01), the Lift is above 1 (i.e. 1/0.01 = 100). Buying item B is very rare (also item A), so if they do both appear in a single transaction, it is very unlikely to happen together, hence there is a strong association, so the Lift from one to the other is large.
Case 2:
P(A) doesn't overlap P(B), then the formulas for Lift simplifies as follow
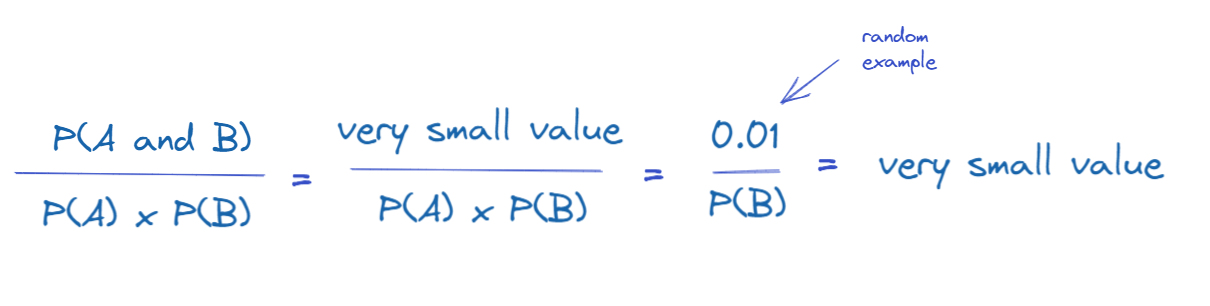
Assume overlap is small, say 0.01. In the case P(B) is large (say 0.9), the Lift is small (i.e. 0.01/0.9 = 0.011). Individually each item are commonly brought, but they are not often brought together.
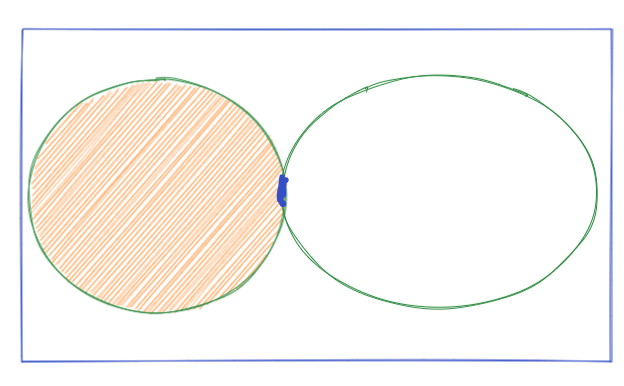
In the case P(B) is small (say 0.01), the Lift is close to 1 (i.e. 0.01/0.01 = 1). Two uncommon items are brought together, they may be associated or may not be, there is not enough evidence to suggest either.
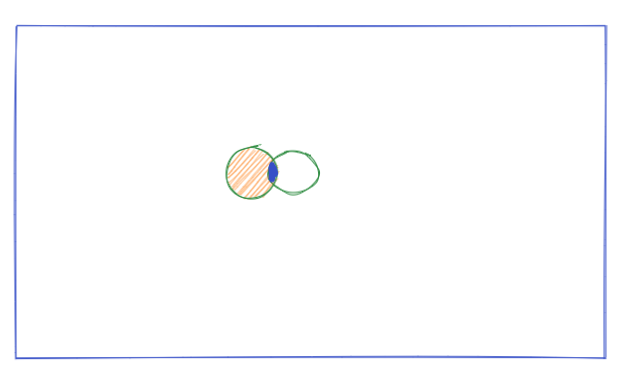
Generally speaking, a large overlap indicates strong association, while the small overlap indicates small association. The result does depends on the probability (frequency of transactions within the total transactions) of buying individual items. In the case of Lift close to 1, it is almost indifferent as buying item A affects buying item B. In the case of large Lift, buying item A are likely to buy/brought item B as well. In the case of small Lift (less than 1), buying item A decrease the likelihood (discourage) buying item B.
Looking for more guides, tips and tricks in Tableau or Alteryx? Go check out the other blog posts from the Data School.
