In this post I will go through how to divide a dataset into quintile intervals, ranked according to a particular numeric field. In the same way the median divides a dataset into two by finding the middle value when ranked according to some field, quintiles are four equally spaced points along the ranked data which together form five intervals that the remaining data can fall into.

Splitting data into quintiles is a useful way to examine the distribution of your data. For example, it can be used see whether the Pareto Principle holds within a chosen dataset.
Now let's get onto finding quintile intervals in Tableau. As an example I chose to work on some anonymised US income data (available here). Each record contains yearly income data for some individual within a sample of the US population. When ranked by yearly income, we are going to calculate the quintile interval each record belongs to. We do this with the following calculated field:

Row by row, this calculated field compares an individual’s yearly earnings to the four quintiles, found using the PERCENTILE LOD functions, to find the quintile interval each person falls into.
Now we are able to split our data by quintile interval in the view. As an example, I put our new Quintile Interval field on columns, SUM(Yearly Earnings) on rows, and then right clicked on this last pill and selected Quick Table Calculation > Percent of Total. This gave me the following chart, from which we can see that the top 20% of earners in the US earn more than the bottom 80% put together.
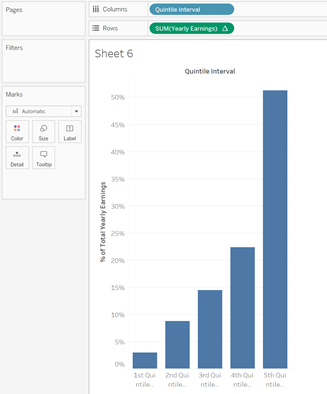
There are some limitations to this method. Because of the way the calculated field is written, we do not necessarily end up with the same amount of data in each quintile interval. In the data above, there were lots of duplicated amounts in the yearly earnings field (a lot of people earned $30,000, for example), and if these happen to be the same as one of the calculated quintiles, they all end up in the same quintile interval, rather than being equitably distributed above and below. I hope to come up with a fix for this in future posts.
