Alteryx stats tools for beginners: part 2 - Data investigation

Alteryx stats tools for beginners

This is part two of a five part series introducing the stats tools available in Alteryx explaining the tools and indicating when their use is appropriate.

Data investigation

Before we get into regression analysis, it is important to investigate the shape of your data.

The data investigation tools

The first stage of any regression analysis should be to investigate the data. The aptly named data investigation tools are great for getting an insight into the shape and characteristics and therefore guiding you in the correct approaches to take and tools to use for your analysis.

Field summary

Use this tool as a starting point if you aren’t already familiar with the structure of the data.

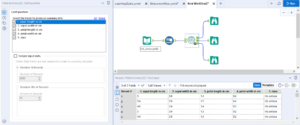
Once you’ve selected which fields you want a summary of, attached browse tools and run it, the O output shows a transposed version of the data, with all the columns headers in separate rows and information about each such as whether values are missing, the minimum and maximum values, standard deviation etc.

The R output gives a report style view of some of the information that was available in the O output.

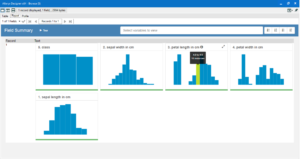
The I output gives a semi-interactive series of histograms displaying the distribution of the data.

It is important that the data type of the fields going into this tool are in the right form, (ie numbers in an integer or double format not as a string etc), I recommend the Auto Field tool directly before the Field Summary tool.

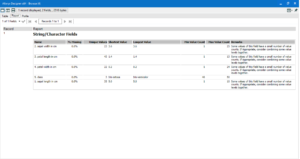
Frequency table

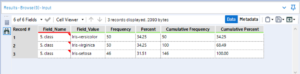
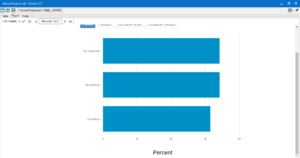
The frequency table tool gives an overview of the number of records for each of the distinct categories within the selected column(s).

Select a field to view, add browses and run.

The D output gives a view of the data in the result window.

The R output gives information in a report style.

The I output is a semi-interactive series of bar charts giving a visual representation of the number of records for each field.

Contingency table

Use this tool to find out the frequency with which two categorical variables occur together. These can be categories/descriptions or binary fields.

The contingency table tool can be used to find the frequency with which two variables occur together, this can be done for up to 4 variables.

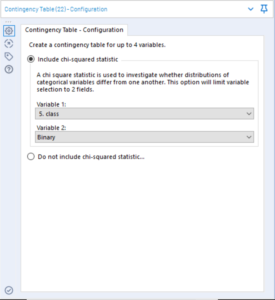
It also has the option to include a chi-squared test (a statistical test which gives and indication of whether the frequency of two variables occurring together is statistically significant), this can only be done on two variables rather than four.

Generally, when using a contingency table to perform a chi-square test, it is advised that for each variable there should be at least a frequency count of 5.

In my data I have added a column which randomly assigns a number between 0 and 5 to each row, so that each class of plant now has 5 sub-classes based on these numbers.

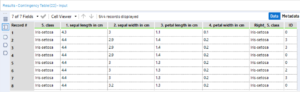
I have run the contingency table, including chi-square statistic, on class and on this number (ID).

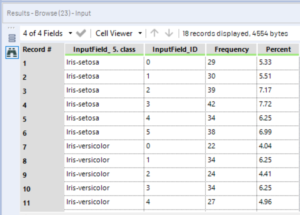
The D output gives a data table with each class broken down by ID, the frequency of fields of each ID per class and a percent of total column.

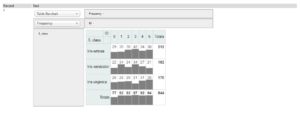
The R output provides a report table of the values included in the data table, and below is listed the chi-squared value, the degrees of freedom, and the p-value of the test.

The chi-square value is used to determine whether the observed frequencies are different to what would be expected to occur to pure chance. It, along with the degrees of freedom, is used to calculate the p-value

The degrees of freedom are the number of values within a calculation which are free to vary, they can be defined as the minimum number of independent variables.

The p-values are a measure of the significance of the findings. Put simply, the p-value is a measure of the likelihood that the results obtained by the test occurred by chance. A smaller p-value is an indication of greater significance. The consensus benchmark p-value is 0.05 (indicating a 95% likelihood that the results are not due to chance) however this is not an absolute value, p-values should be taken as an indicator of how much to trust the results.

The I output provides an interactive chart that enables you to select a visualisation format and a measure to represent.

It is important to note that predictor variables should not correlate with one another; they should each be as independent as possible from one another, if they correlate well with one another then they are probably not both needed in the predictive model.

Distribution analysis

Use this tool when you want to see how a continuous variable is distributed and compare it different types of distribution curves.

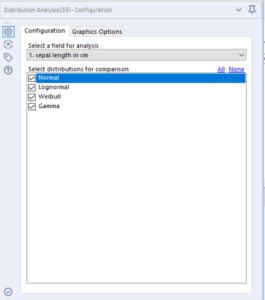
Only one variable can be chosen at a time and compared to up to four distribution curves.

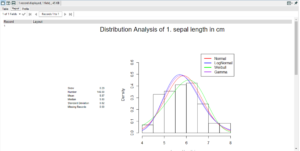
The output shows a distribution histogram of the variable selected with the selected distribution curves overlaid.

Beneath that is a goodness of fit table, as stated below the chi-square test is the best indicator of goodness of fit; the lower the significance the more likely it is that that curve will fit the distribution and the higher the statistic value the better the fit.

The distribution is important when selecting the most appropriate regression analysis tool to use.

Association analysis

Use this when you want to get an overview of how a number of continuous variables associate with one another in a bivariate manner (analysing how all the selected variables associate with each other selected variable).

Select the variables you wish to analyse. You are given the option to target a field for a more detailed analysis, if you select this a drop-down box will appear to enable you to select the measure you want to target, and you will have to input the ‘target level of interest’. The field for targeted analysis must have only two values (e.g. binary, yes or no, win or lose etc) for this to work, and you must specify one of the values as the ‘target level of interest’ (e.g. ‘win’)

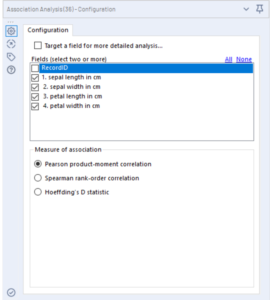
The measures of association that you select will determine in what manner the association is measured. There are three options available in this tool: Pearson product-moment correlation; Spearman rank-order correlation; and Hoeffding’s D statistic.

You should use Pearson when you know that the fields have a linear relationship (they both increase or decrease at roughly the same rate as each other).

You should use Spearman when you know that the fields have a monotonic, but non-linear relationship (they both increase in the same direction but not necessarily at the same rate).

You should use Hoeffding’s when you know that the fields have a non-monotonic relationship (they don’t necessarily increase in the same direction or at the same rate, but there is a definite pattern to the relationship).

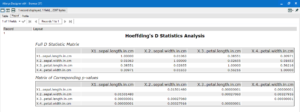
Once you have selected the fields and the measure of the association, attach browse tools and run the workflow. The R output will give a report style view with a correlation matrix table and a table below with corresponding p–values.

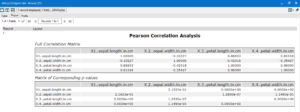
The closer the correlation matrix value is to 1, the stronger the positive relationship between the variables. There will always be a diagonal row of 1’s running top left to bottom right, as this is where each variable has been compared to itself and will always have a 1:1 association. The closer to -1, the stronger the inverse relationship (one increases and the other decreases). The Hoeffding’s D statistic will never be negative, because it does not assume a direction to the relationship.

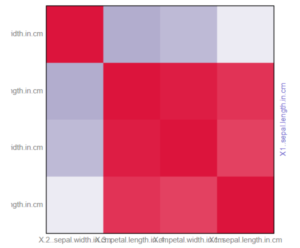
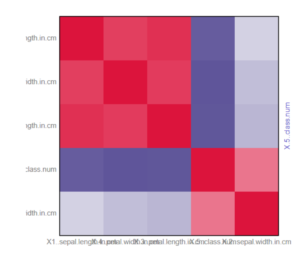
The I output provides an interactive heatmap of the correlation matrix; the deeper the shade of red the stronger the positive relationship between the two measures, the deeper the shade of purple/blue the stronger the inverse relationship. As above, there will be a diagonal line of deep red due to the 1:1 relationship of variables with themselves.

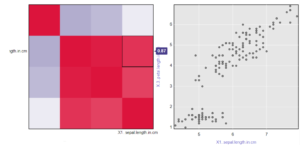
Clicking on a square within the heatmap will load a scatterplot on the right that plots the two variables against one another with each row of data making up a point on that plot.

If you checked the target field box and inputted a target level of interest the R output will contain an extra table at the top, with a focused analysis of how each measure associates with the target and a corresponding p-value.

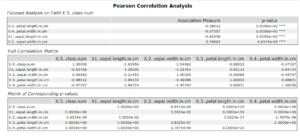
The I output will look slightly different, as it will now include the target field and how each of the variables associates with it.

Scatterplot

Use this when you want to visualise how two variables compare to one another; each point on the plot represents a row of data containing those two fields.

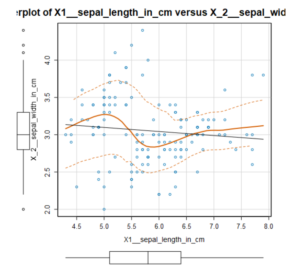
Under the plot elements tab of the configuration window, you can select whether to include a regression line (a linear trend line), a smooth line (a slightly curvy trend line); you can also add boxplots to sit outside the axis, you can jitter the points (recommended if one of the axes is categorical, or the majority of points sit bunched around a single value.

The output will give a report style chart with the data points, the regression lines and the box plots outside the axes if you chose to include them.

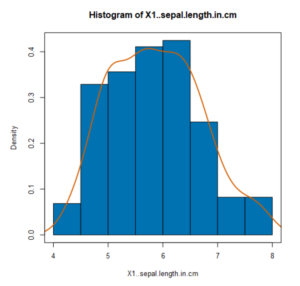
Histogram

Use this when you want to see the shape and spread of continuous data. A histogram groups a continuous variable into ‘bins’ of a fixed size and presents the number of data points that fall into each bin by the height of bars.

Select the continuous variable you want to see the distribution, you can input a set number of ‘breaks’ (bins) into the tool or leave it at auto; there is also the option to plot a smoothed density curve over the top of the histogram.

The output will provide a bar chart representation of the distribution of values within the bins; the higher the bar the more fields that lie within that range.

Plot of means

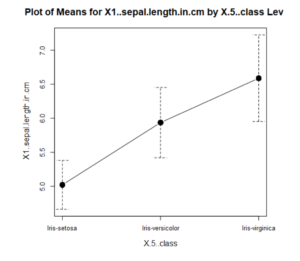
Use this when you want to see how the median of a single continuous variable compares across different categories. The median is a type of average calculated such that a variable has equal likelihood of being above or below it, in other words 50% of the values lie on either side of the median. There is the option to include error bars, which give an indication of the spread of the data around that median.

Select a continuous variable and a categorical variable to group it by. Standard error is an estimate of how far the mean of your samples lies from the mean of a larger population. Standard deviation is the degree to which individual values within your sample lie from the sample mean. Confidence interval is the percentage likelihood that a random additional value in that sample would lie within the defined range. The confidence interval can be set, however 95% is generally accepted as gold standard.

The output gives a plot of where the mean of the variable lies for each category (the solid points) and the selected error bars (the dashed lines).

I hope this was useful for finding some relationships within and between parts of your data; much of this will feed into the next section on regression analysis, where the tools you choose are heavily influenced by shape of your data.

Part 3 on regression analysis here.

Author:

Andrew Lehm

View Profile