Alteryx stats tools for beginners
This is part three of a five part series introducing the stats tools available in Alteryx explaining the tools and indicating when their use is appropriate.
- Clustering
- Data investigation
- Regression analysis
- Classification
- Time Series Analysis
Regression analysis
Regression analysis is, at its core, a method for investigating the relationships between two or more variables of interest. There must always be one dependent (target) variable (the variable we want to see influenced) and at least one independent (predictor) variable (the variable(s) we want to see the influence of on the dependent variable). Regression analysis can also indicate the strength of impact of multiple predictors on the target variable.
There are two main classes of regression analysis tools: those that are designed to deal with discrete dependent variables (such as those sorted into categories, binary etc) and those suited to dealing with continuous dependent variables (a continuous measure without any gaps such as size, income, duration etc).
While a form of regression is used for forecasting or time series analysis, there are a number of tools specifically for this in Alteryx which we will look at in detail later in the series; this section will focus on analysing causal effect relationships between variables.
A brief aside: one important fact to note, and one that is often brushed over or forgotten, is that statistical analysis, regression analysis included, can only ever indicate correlations between factors, not causal relationships. Regression analysis is a great technique for making predictions and understanding the influences of variables on one another, but are sometimes misused, or misunderstood, and taken to be a reliable proof of causality. This is misleading. While some of the variables included in a regression model may very well be causally related to one another, they also might not be; without empirical testing, these relationships cannot be taken as absolute. This is something that I feel strongly about; one of the main reasons I am writing this series of blogs is to help people use these tools with the proper understanding of how they work, what they can be used for, and how much to believe the results they provide us with. I’d like to thank Brian for raising his concern on this, and encouraging me to add this paragraph for clarification.
Regression modelling
The basic schema for the process of regression analysis is to build a model based on your existing data (with predictors and target variable), to test that model against data for which we know the target variable (this will give us an idea of how reliable the predictions of the model are) and then to use to model to predict the target variable for new data.
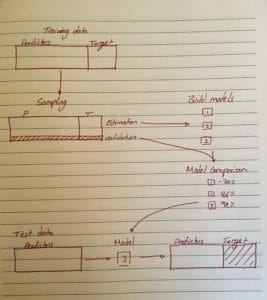
Regression model schema
Data preparation
But before we can begin with this process we need to establish a few key facts about the shape of the data.
We need to establish whether the target variable is continuous, categorical or binary; whether the data is normally distributed or not, whether there are nulls within the data, or whether any of the variables we are going to use as predictors are interrelated.
In my previous blog post I went through the data investigation tools, which are extremely useful for this step.
It should be pretty simple to establish whether the target variable is continuous (eg. sales), categorical (North, South, East or West), or binary (yes/no, true/false) just by looking at the data, but we can also use the field summary tool, as this will also provide some insight into whether any of the predictor variables have values missing and the number of unique values for each predictor.
Nulls
Regression analysis cannot handle nulls, so it is important to decide how to deal with them or when to exclude a variable if there are too many nulls. There are methods we can use to fill in a small number of blanks, so that we don’t have to lose an entire variable, but this has its limits. Personally, I wouldn’t include a predictor with more than 20% of values missing as I feel that any insight gained from it is likely flawed due to the fabrication of data. However, this depends on the data at hand, if I have relatively predictable data (i.e. some sales figures are missing but I have data on the number of customers) I might run an association analysis, check if there is a linear relationship between the two and then use that assumption to fill in a number of values. However if my data is wildly unpredictable, I will feel less comfortable making such assumptions and therefore be less likely to fill in so much data.
We can then make the choice whether to simply exclude the entire variable, or to exclude the rows which contain nulls for any of the variables.
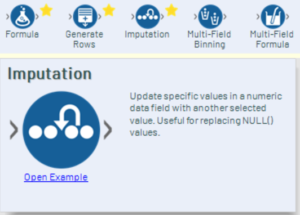
If the amount of nulls is small enough, the imputation tool is super useful for filling in these gaps.
Collinearity
This flows well into the next issue, which is checking whether any of the predictors are interrelated. As I mentioned above, I can use the association analysis to see the relationship between number of customers and sales figures; if this relationship were very linear, I could likely assume that one has either a causal relationship on the other, or they are both causally influenced by another, perhaps unknown, variable. It is then probably advisable to include only one of the two variables in the model. Having collinear variables in a model can make a model hypersensitive to fluctuations.
For example, if my model is based on sales figures and number of customers data, and my number of customers drops, it follows that my sales figures will probably also drop; if my model applies a weighting to both sales figures and number of customers figures, this will exhibit itself as a double drop in the model, when in actuality there is a single cause being represented twice by the two variables. However, if my model is based on number of customers data and bee population data, it is unlikely that a change in either of the two will have a direct knock on effect on the other; bee numbers are unlikely to decrease due to a reduction in customers at a superstore.
We can run the association analysis tool on all of our predictor variables (and can even include the target variable in the analysis, to exclude variables which seem to have no association with the target at all) and decide to trim down our pool of variables. There is also the option to do this after having built your model, and to compare the more pared down models with the original model with full data.
Collinear variable removal
I have sales data for a number of stores and then I have demographic data about the areas around those stores. I am going to use this information to decide where might be the best location to open a new store, based on demographic information I have collected about a number of potential locations.
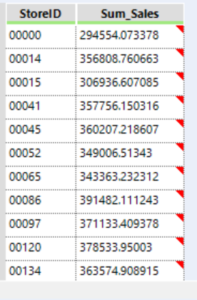
Sales data
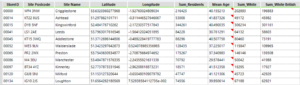
Demographic census data
I am going to join the data sources, check that the data is in the right format (numbers as numerical and text as strings) and then run an association analysis. I am going to target it at Sum_sales as I want to see whether any variables have little impact on this, allowing me to pare down my model.
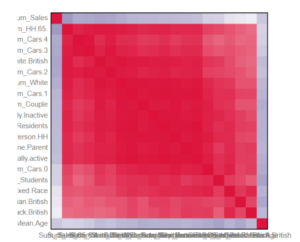
Let’s take a look at the I output first, and we see a large chunk of bright red, except around the outside, where the association of the other variables with Sum_sales is fairly low. This indicates that there is no single variable which strongly influences the target (sales), but that many of the predictors are interrelated.
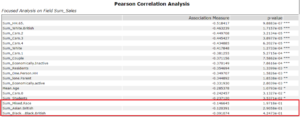
If we then look at the D output, we can see this association displayed numerically. I am going to use the focused analysis to eliminate some variables that don’t seem to have much of an influence; the bottom three have low association measures and high p-values so I will eliminate them from my model.
I now want to start eliminating collinear variables from my analysis. I have decided that 0.9 is my cutoff point for collinearity, so any two variables that have a value greater than 0.9 (or less than -0.9) in the correlation matrix I will note down so I can decide which one of the two to remove.
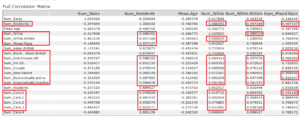
Ok, that’s quite a lot of variables to remove, perhaps I’ll limit it to only those above 0.99 for removal; this stage can require some playing around and perhaps even building a model with each and comparing them.
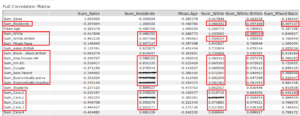
Using a select tool, I can reduce the number of predictor variables that are going to feed into my model.
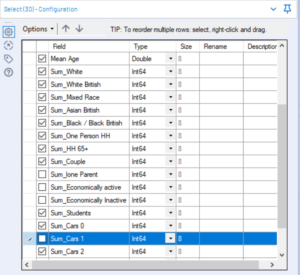
Distribution
Another thing to address is the distribution of the predictor variables. While the analytical models do not need the data to be normally distributed, it is often useful to be aware of the shape of the data, of any influential outliers or the effects that a skewed distribution of data might have on the model. In some cases it might be useful to transform or normalise the data in order to improve the model.
Building a model
Now that we have examined and prepared our data for regression, it is time to start building the model.
Sampling
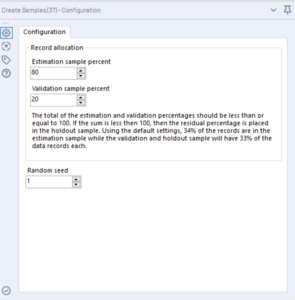
The first stage is to divide our data into two samples, one for the construction of the model and the other for testing the model. A general rule of thumb is to have 80% of your data in the estimation sample and 20% for validation.

The create samples tool can split your data into estimation and validation populations
Choosing models
If your target variable is continuous you can use the following models:
- Boosted model
- Count regression (limited to small, positive integers (i.e whole numbers between 1-10)
- Decision tree
- Forest model
- Gamma regression (limited to positive variables with a long right-hand tail (a small number of extremely high values and a large number of relatively low values)
- Linear regression
If your target variable is discrete you can use the following models:
- Boosted model
- Decision tree
- Forest model
- Logistic regression
- Naive Bayes classifier
This blog post will focus on continuous data, for a run-through of analysing categorical data see the next section on classification (coming soon).
In my case, the target variable is continuous. I generally use all of the applicable models and then compare them to find the best. Given the shape of my data, I am going to be using the boosted, decision tree, forest, and linear regression models.
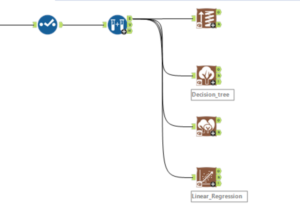
I am going to configure them all so that the target variable is Sum_sales and that they use only the relevant predictors (I am excluding store ID from the model).
Comparing models
I am then going to union all of the O outputs together compare the models using the model comparison tool.

Attach the output of the union to the M input of the model comparison tool and the verification output from the create samples tool to the D input. The tool requires configuration only if the target variable is a specific categorical option (eg. yes out of yes/no).
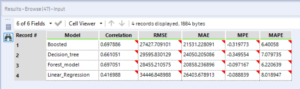
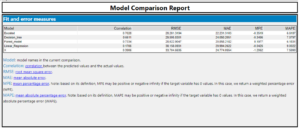
The E output shows the correlation (of each model’s predicted values with those in the validation sample), the RMSE (root mean square error), MAE (mean absolute error), MPE, (mean percentage error), MAPE (mean absolute percentage error). Generally, the smaller the RMSE the better.
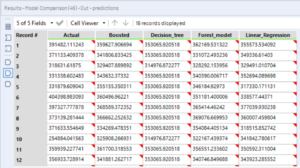
The P output shows the actual value from the validation sample, next to the predictions from each of the models.
The R output gives a report style representation of the data.
Side note: tweaking
In the interests of analysis, I ran the models again, but this time without excluding the variables that I established has close association with others. The results showed that the correlation was slightly higher, but so too was the RMSE. This seems in line with the earlier explanation: while they enable the model to more closely fit the existing data, the model is then more prone to variability in the results, which can lead to predicted values which are further from the real data.
The stepwise tool is useful for removing unnecessary predictor variables from some models (limited to linear, logistic, gamma, and count regression models). I have used it here on the linear regression model to see if it can improve it.
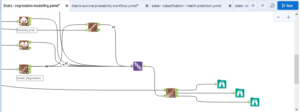
To use the tool, connect the O output from an applicable model to either one of the inputs, and the estimation sample used to create the model to the other input.
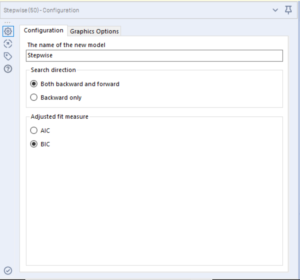
The search direction describes whether the model will test the significance of the predictors in a backward only direction (starting with all and removing one by one) or in a forwards direction (adding variables in at each step). This option is labelled backwards then forwards, as it always starts with a backwards step.
The adjusted fit measures refer to the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). These two measures are similar to one another, but the BIC places a larger penalty on the number of variables included in the model, typically resulting in a final model with fewer variables than is the case when the AIC is used.
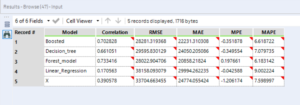
I have then unioned the O output to the others and run this through the model comparison tool.
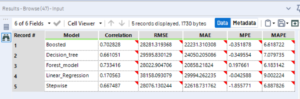
The stepwise tool results in a massive improvement in the correlation value over the linear regression tool, as well as massively reducing the RMSE. I would advise running this tool on all applicable models.
Model testing
The final stage of regression analysis is to run the model on new data. This is done using the score tool.
Since we have decided that the boost model is the best for this situation, I am going to add all of the other models, as well as the model comparison tool, to a container and disable it.
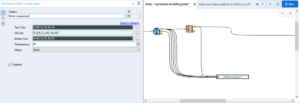
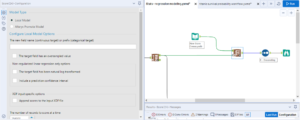
I will input my new data, and use the score tool. Attach the O output from your best model to the M input of the score tool, and your new test data to the D input. The default configuration of the tool is usually fine.
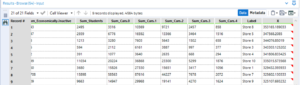
The tool predicts a target value (X) for the new data we have provided it with. In my case I am trying to decide where a store will be most profitable. Because I don’t trust that the model contains all of the variables that go into deciding store profitability, I am going to select the top 5 using the model and suggest these, as there may be other considerations that will impact a store’s success. This is something that the shareholders will probably have knowledge of.
I hope this post, and the series so far, have been useful. Part 4 on classification here.
