Revelations – densification using bins and Index in Tableau. Case in point: normal distribution.

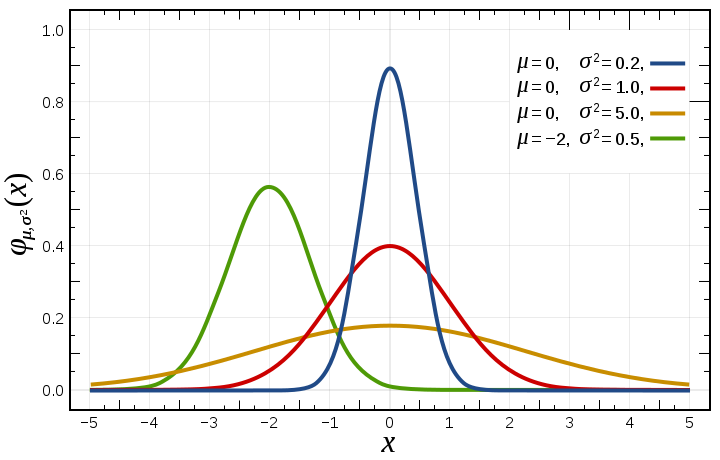
wikipedia's different normal distributions - densification examples

Normal Distributions as an example of equations to draw via densification. Image from Wikipedia.

TL;DR: Bins, index and densification can help twisting and wobbling lines. A Sankey is just a slope chart―only the lines are not straight.

This week was “Teaching week” at the Data School. Each of us taught about a topic that either interested us or that we needed some reinforcement with. Jeremy taught us about Sankeys. How to build them with a step-by-step guide and a couple of revelations. It was an eye-opener.
It took me a while, despite Jeremy’s best efforts, to grasp the concept of densification; how to use the bins to set the boundaries, and how to use Index() to account for the missing values between the boundaries. But, thanks to Jeremy’s examples ―and to some further digging― I understand it a little better now, and possibilities are just starting to emerge (case in point, let’s build a tool to plot a normal distribution graph).

Revelations:

To build a Sankey, you need three calculations:
1. The first one, to set the beginning.
2. The second one, to set the end.
3. The third one, to tell tableau how to connect the beginning and the end.
Once you know your beginning and your end, you can connect them almost any way you want including, why not, the bell-shaped normal curve.

Normal Distribution

My goal: to build a simple normal distribution from its parameters –mean & standard deviation― as opposed to from actual data (which Robin Kennedy has shown already).
I know the beginning (0), and the end (0), and the formula to plot it:

What I need to produce the curve is to be able to apply the above formula along the x-axis, whose values should be more or less around the mean (to be able to capture the bell shape they should start from ~ 6 SD around the mean).

Densification

I start with a dataset that has a single row with one single (dummy) value.

Connecting in Tableau to that table, and unioning it to itself yields the following table:

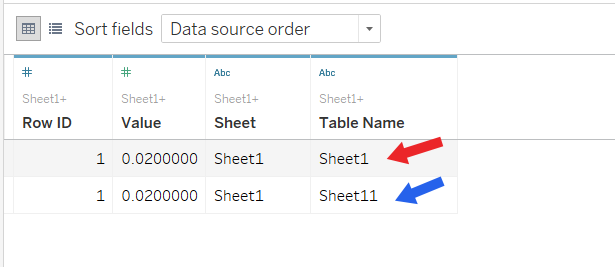
This step could have been replaced by using a datasource with two rows, each with a unique identifier, but the idea of duplicating the datasource will be useful in other graphs – Sankey, for instance.

I am going to use one row as the beginning of my curve, and the other as the ending:

For the beginning, I will use:

minimum value as a function of the parameters

Notice everything is purple: parameters to configure the curve and extension of the axis.

And for the ending, the same approach, but adding the standard deviations instead of subtracting them.

To assign them to the different rows, an IF statement over the unique identifier (in this case, “Table Name”)

So far, this looks like:

Two rows, different calculations. No magic so far.

Bins

And now, the first revelation: creating bins makes Tableau self-aware of the gaps.

Create bins of X size (~1/10 or 1/100 of the SD should work)
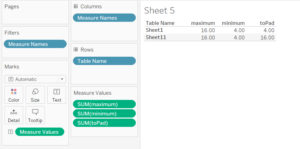
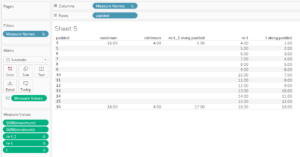
Put the recently created bins on rows and show the minimum & maximum (based on the parameters created: average = 10, stdev = 1, bin size = 1, number of sd to show =6)

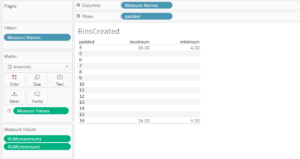
initial calculations shown only on bins with data

Only the rows with underlying data (in the first and last bin) show the maximum and minimum (the only two existing calculations so far).

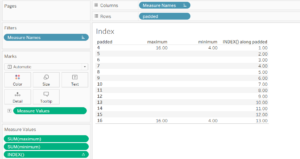
Now, adding “INDEX()” (and making sure it is computing using the bins (“padded”)) to Measure Values:

Index() correctly numbers even bins with no data

Tableau is aware of the gaps, and Index() correctly numbers them.

How can this be used to plot the curve of interest?

We have the equation for the curve, we have now a serialized sequence between the starting and the end points -aka the index. The only thing needed is to “re-scale” the index so that it is bounded and regularly spaced:

Write the equation.
Re-scale the index

Re-scaling the index:

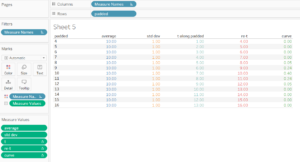
Right now, the index goes from 1 to 13 (from the smallest to the largest bin). Ideally, it should follow the same numbers as the bins (“padded”). To re-scale it: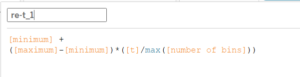

This takes the starting point (minimum) and grows gradually in each step until it reaches the latest bin (at the maximum). This is, effectively:
y = mx + c
where y is the re-scaled index;
x is t (the renamed “Index”); c = minimum and m = (maximum – minimum)/number of bins.

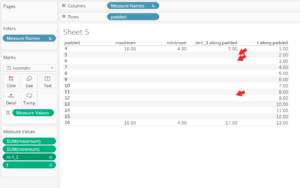
Adding the newly calculated field to the table:

Well, that didn’t work as expected.

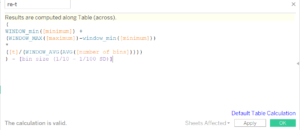
The first and the last values are almost OK, just need to be adjusted by one “bin size”, but none of the intermediate steps are computing properly. Why? The reason is the equation of the recoded index relies on “minimum” and “maximum”, but those calculations only take place on the bins that have underlying data. To account for the missing values, the equation needs to be amended to use table calculations:

Using table calculations allows using the equation for bins with missing values.

And, in the table:

The re-scaled index “re-t” now properly working.

Equation

Now the only thing pending is to plug in the equation for the normal distribution from above:

A word of caution: PI(), needed for the computation, is also a calculation. Which means it will not be accessible for those bins with missing data –it will only work for the boundaries. Table calculations, once again, to the rescue–and we can write the equation as:

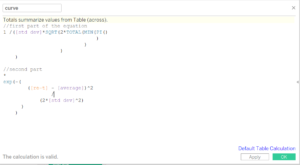
To be able to use PI() for all the points, the table calculation is needed. Note that table calcs are not needed to obtain the values from the parameters.

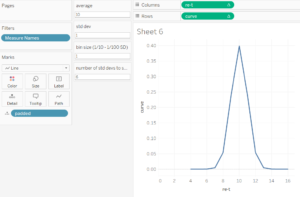
And building the table:

crosstab with values for index and curve

The curve values seem ok, if a bit scarce.

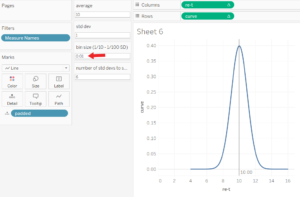
When plotted:

That looks “normalish”, but with a very steep step.

Smoothing via reducing bin size and:

A “proper” normal distribution built from its mean and standard deviation!

Re-cap:

The underlying data is a table with two records (here a single row with a dummy value unioned to itself).
Minimum and maximum values define the limits of the bins.
A parameter defines the size of the bins.
Bins make Tableau self-aware of missing points/
That can be used via INDEX()
And applied to whatever formula (in this case, the density function of the normal distribution).
A working example: