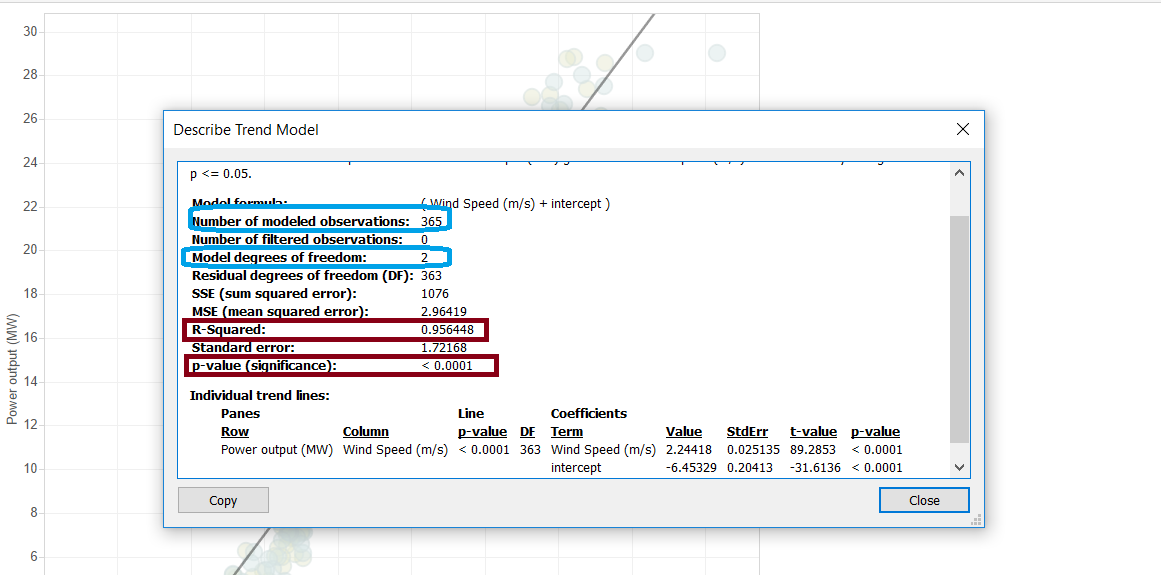
Sometimes when using a Linear Regression to analyse our data, we may think that the model we are using is the best fit for our data because the p-value is significant (p-value< 0.05) and the r-square value is close to 1 (R² is high), however this may not always be the case. We should always assess the appropriateness of the model by defining the residuals and examining the residual plots.
But what is a residual?
A residual is the difference between the observed value of the dependent variable (y) and the predicted value (ŷ). Each data point has one residual.
Residual = Observed value – Predicted value
e = y – ŷ
Note: The sum and the mean of the residuals are equal to zero.
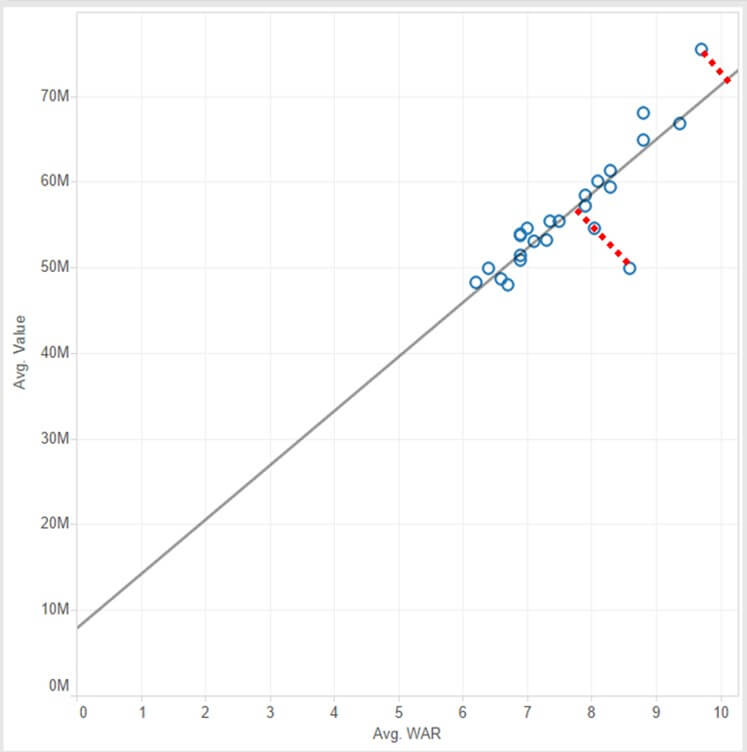
And a residual plot, what is it?
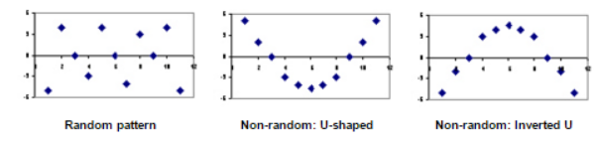
A residual plot is a graph that shows the residuals on the vertical axis and the independent variable on the horizontal axis. If the points in a residual plot are randomly dispersed around the horizontal axis, this means that our linear regression model is appropriate for the data; otherwise, a non-linear model is more appropriate.
The residual plots show ‘two typical’ patterns: a random pattern (indicating a good fit for a linear model) and a non-random pattern (U-shaped and inverted U), suggesting a better fit for a non-linear model.
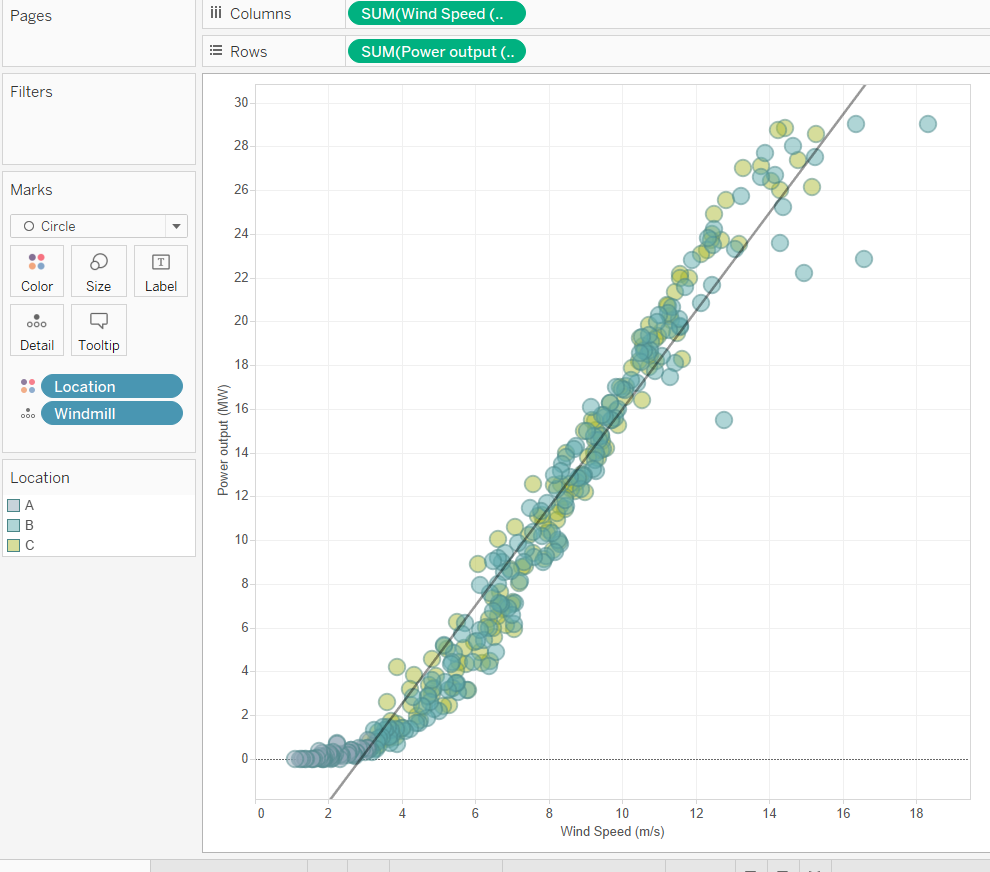
How do we do a residual plot in tableau?
1 – On the sheet that you have visualised your scatterplot, go to worksheet menu and select export data
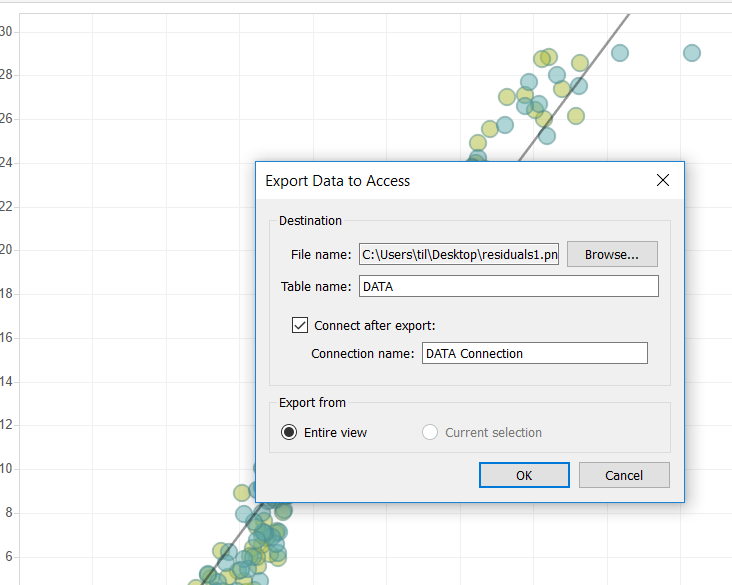
2 – On the menu box select ‘Connect after Export’ and click OK (this will now be saved as an Access file and it will open automatically in Tableau)
3- On a new sheet, drag the recently created field ‘residuals’ to the rows and your independent variable to columns (x axis) – in this example ‘wind speed’
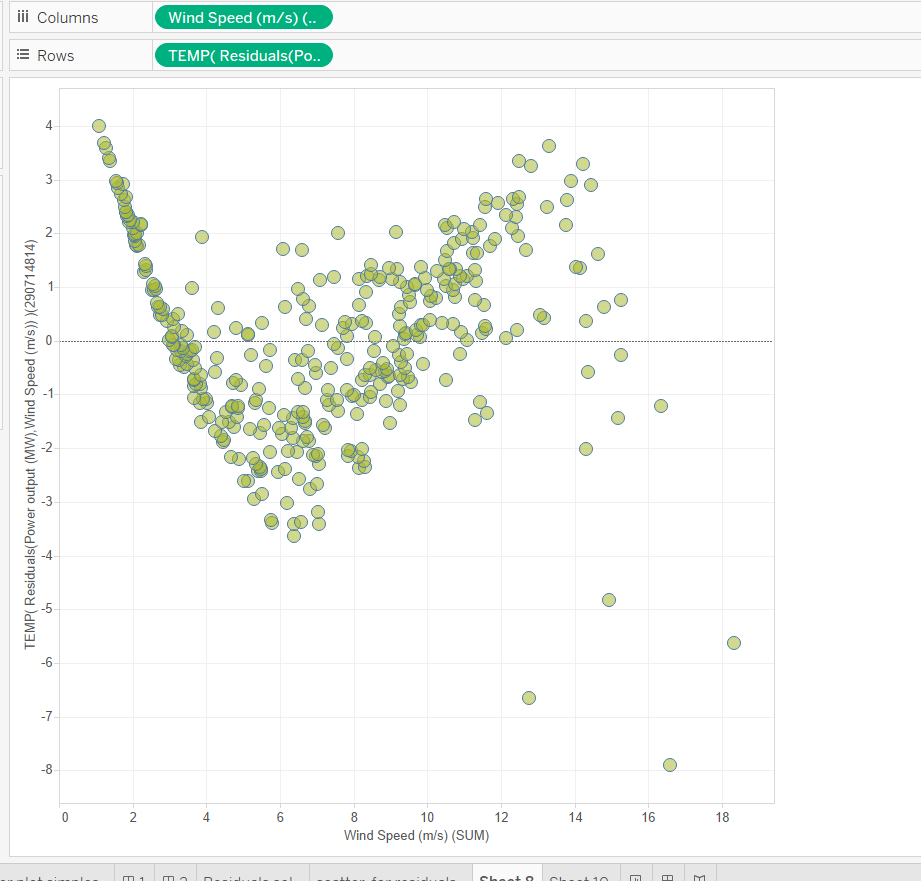
- We can now see that the residuals aren’t randomly distributed, they do follow a pattern – a ‘sigmoid distribution’. This tell us, that contrary of what we believed (by analysis of p-value and r-square) the Linear Regression model isn’t the best fit model to our data. We should now look for other types of models, namely the non-linear models.
Example of a residual plot showing that our linear regression model is the best fit to our data 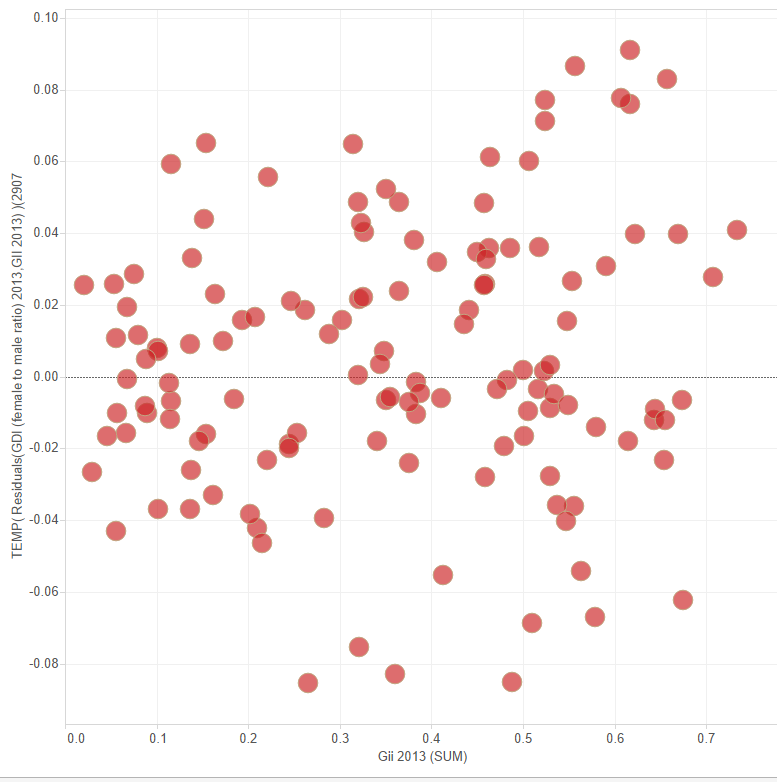
Random Distribution around zero
Note: when accessing p-value and R-squared don’t forget to analyse the number of observations and degrees of freedom, as these may indicate an artificially high r-squared value.
High number of observations and low degrees of freedom indicate that the high r-square value may be due to external reasons.